在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：
，过点P（-2，-4）的直线
的参数方程为
（t为参数）与C分别交于M，N.
（1）写出C的平面直角坐标系方程和的普通方程；
（2）若
，
，
成等比数列，求a 的值.
已知
、
、
为
的三内角，且其对边分别为
、
、
，若
．
（1）求；
（2）若
，求的面积．
已知双曲线的中心在原点，焦点在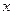
轴上，离心率
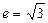，焦距为
（1）求该双曲线方程.
（2）是否定存在过点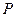
，
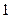）的直线
与该双曲线交于
，
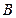两点，且点
是线段
的中点？若存在，请求出直线的方程，若不存在，说明理由.
设
、
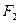分别是椭圆
的左、右焦点.
（1）若
是该椭圆上的一个动点，求
·
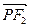的最大值和最小值;
（2）设过定点
的直线
与椭圆交于不同的两点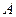
、
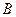，且∠
为锐角（其中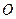
为坐标原点），求直线的斜率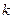
的取值范围.
某承包户承包了两块鱼塘，一块准备放养鲫鱼，另一块准备放养鲤鱼，现知放养这两种鱼苗时都需要鱼料A、B、C，每千克鱼苗所需饲料量如下表：
| 鱼类 |
鱼料A |
鱼料B |
鱼料C |
| 鲫鱼/kg |
15g |
5g |
8g |
| 鲤鱼/kg |
8g |
5g |
18g |
如果这两种鱼长到成鱼时，鲫鱼和鲤鱼分别是当时放养鱼苗重量的30倍与50倍，目前这位承包户只有饲料A、B、C分别为 120g、50g、144g,问如何放养这两种鱼苗，才能使得成鱼的重量最重．
若过点
和B
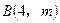并且与
轴相切的圆有且只有一个，求实数
的值和这个圆的方程。