如图,在正方体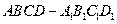 中,
中,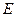 是
是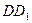 的中点,
的中点,
求证: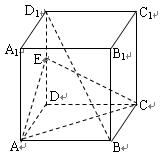
(1)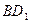 ∥平面
∥平面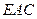 ;
;
(2)求异面直线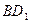 与
与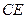 所成角的余弦值.
所成角的余弦值.
(本小题满分14分)已知函数 是一次函数且在
是一次函数且在 上为增函数,若
上为增函数,若 .
.
(Ⅰ)求 的解析式;(Ⅱ)试比较
的解析式;(Ⅱ)试比较 与
与 的大小.
的大小.
已知

 ,复数
,复数 ,当
,当 为何值时,
为何值时,
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 是纯虚数;(Ⅲ)
是纯虚数;(Ⅲ)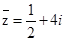 .
.
(本题满分14分)已知集合
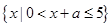 ,集合
,集合

(Ⅰ)若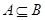 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)若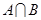 是单元素集合求实数
是单元素集合求实数 的值.
的值.
(本小题满分14分)
设函数 .
.
(Ⅰ)当 时,求函数
时,求函数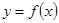 的单调区间;
的单调区间;
(Ⅱ)已知 ,若函数
,若函数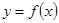 的图象总在直线
的图象总在直线 的下方,求
的下方,求 的取值范围;
的取值范围;
(Ⅲ)记 为函数
为函数 的导函数.若
的导函数.若 ,
,
试问:在区间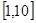 上是否存在
上是否存在 (
(
 )个正数
)个正数 …
… ,使得
,使得 成立?请证明你的结论.
成立?请证明你的结论.
(本小题满分12分)
函数 .
.
(Ⅰ)若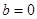 ,且
,且 在
在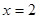 处取得极小值,求实数
处取得极小值,求实数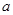 的值;
的值;
(Ⅱ)若函数 在
在 上是增函数,试探究
上是增函数,试探究 应满足什么条件;
应满足什么条件;
(Ⅲ)若 ,不等式
,不等式 对任意
对任意 恒成立,求整数
恒成立,求整数 的最大值.
的最大值.