(本小题满分12分)已知在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。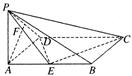
(1)求证:AF//平面PEC;
(2)求PC与平面ABCD所成的角的大小;
(3)求二面角P—EC—D的大小。
在 中,
中, 、
、 、
、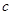 分别是三内角A、B、C的对应的三边,已知
分别是三内角A、B、C的对应的三边,已知
(1)求角C的大小;
(2)满足 的
的 是否存在?若存在,求角A的大小.
是否存在?若存在,求角A的大小.
在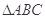 中,内角
中,内角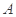 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,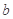 ,
, ,已知
,已知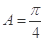 ,
, =
=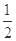
 .
.
(1)求 的值;
的值;
(2)若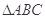 的面积为3,求
的面积为3,求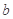 的值.
的值.
设函数f(x)=ln +
+ (a>0).
(a>0).
(1)若函数f(x)在区间(2,4)上存在极值,求实数a的取值范围;
(2)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(3)求证:当n∈N*且n≥2时, +
+ +
+ +…+
+…+ <ln n.
<ln n.
已知椭圆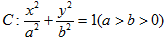 的离心率为
的离心率为 ,以原点
,以原点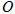 为圆心,椭圆
为圆心,椭圆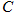 的长半轴为半径的圆与直线
的长半轴为半径的圆与直线 相切.
相切.
(1)求椭圆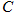 标准方程;
标准方程;
(2)已知点 为动直线
为动直线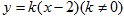 与椭圆
与椭圆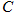 的两个交点,问:在
的两个交点,问:在 轴上是否存在点
轴上是否存在点 ,使
,使 为定值?若存在,试求出点
为定值?若存在,试求出点 的坐标和定值,若不存在,说明理由.
的坐标和定值,若不存在,说明理由.
已知函数 在(1,+∞)上是增函数,且a>0.
在(1,+∞)上是增函数,且a>0.
(1)求a的取值范围;
(2)求函数 在[0,+∞)上的最大值;
在[0,+∞)上的最大值;