(22、23、24三题中任选一题作答,如果多做,则按所做的的第一题记分)
(本小题满分10分)选修4—4:坐标系与参数方程已知直线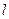 的参数方程为
的参数方程为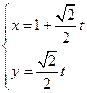 (
(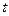 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是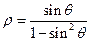 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点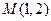 ,直线
,直线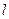 与曲线C交于A、B两点.
与曲线C交于A、B两点.
(1)写出直线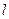 的极坐标方程与曲线C的普通方程;
的极坐标方程与曲线C的普通方程;
(2) 线段MA,MB长度分别记为|MA|,|MB|,求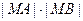 的值.
的值.
(本小题满分12分)
已知函数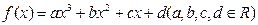 ,且函数
,且函数 的图象关于原点
的图象关于原点
对称,其图象在x=3处的切线方程为
(1)求 的解析式;
的解析式;
(2)是否存在区间[m,n],使得函数 的定义域和值域均为[m,n],且其解析式为
的定义域和值域均为[m,n],且其解析式为 的解析式?若存在,求出这样一个区间[m,n];若不存在,则说明理由.
的解析式?若存在,求出这样一个区间[m,n];若不存在,则说明理由.
(本小题满分12分)
双曲线 ,一焦点到其相应准线的距离为
,一焦点到其相应准线的距离为 ,过点A(0,-b),B(a,0)的直线与原点的距离为
,过点A(0,-b),B(a,0)的直线与原点的距离为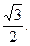
(1)求该双曲线的方程
(2)是否存在直线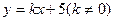 与双曲线交于相异两点C,D,使得C,D两点都在以A为圆心的同一个圆上,若存在,求出直线方程;若不存在说明理由.
与双曲线交于相异两点C,D,使得C,D两点都在以A为圆心的同一个圆上,若存在,求出直线方程;若不存在说明理由.
本小题满分12分)
|
已知斜三棱柱ABC—A1B1C1, 在底面ABC上的射影恰为AC的中点D,又知
在底面ABC上的射影恰为AC的中点D,又知
设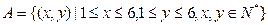
(1)求从A中任取一个元素是(1,2)的概率;
(2)从A中任取一个元素,求 的概率
的概率
(理)(3)设 为随机变量,
为随机变量,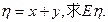
(2)设从A中任取一个元素, 的事件为C,有
的事件为C,有
(4,6)(6,4)(5,5)(5,6)(6,5)(6,6)
(本小题满分10分)
已知不等式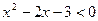 的解集为A,不等式
的解集为A,不等式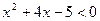 的解集为B,
的解集为B,
(1)求
(2)若不等式 的解集是
的解集是 ,求
,求 的解集.
的解集.