(本小题满分12分)
某企业为适应市场需求,准备投入资金20万生产W和R型两种产品.经市场预测,生产W型产品所获利润 (万元)与投入资金
(万元)与投入资金 (万元)成正比例关系,又估计当投入资金6万元时,可获利润1.2万元.生产R型产品所获利润
(万元)成正比例关系,又估计当投入资金6万元时,可获利润1.2万元.生产R型产品所获利润 (万元)与投入资金
(万元)与投入资金 (万元)的关系满足
(万元)的关系满足 ,为获得最大利润,问生产W.R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元)
,为获得最大利润,问生产W.R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元)
设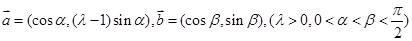 是平面上的两个向量,若向量
是平面上的两个向量,若向量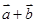 与
与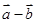 互相垂直.
互相垂直.
(Ⅰ)求实数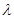 的值;
的值;
(Ⅱ)若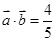 ,且
,且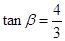 ,求
,求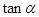 的值.
的值.
已知数列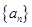 的前
的前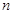 项和为
项和为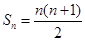 .
.
(Ⅰ)求数列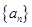 的通项公式
的通项公式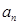 ;
;
(Ⅱ)记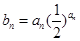 ,求数列
,求数列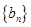 的前
的前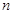 项和
项和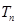
如图,两矩形ABCD,ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.
(1) 求证:MN丄平面ABCD
(2) 求线段AB的长;
(3) 求二面角A—DE—B的平面角的正弦值.
设函数 ,若函数在点
,若函数在点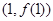 处的切线为
处的切线为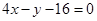 ,数列
,数列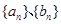 定义:
定义: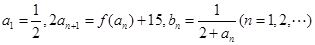 。
。
(1)求实数 的值;
的值;
(2)若将数列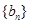 的前
的前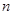 项的和与积分别记为
项的和与积分别记为 。证明:对任意正整数
。证明:对任意正整数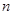 ,
,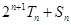 为定值;证明:对任意正整数
为定值;证明:对任意正整数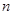 ,都有
,都有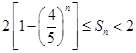 。
。
已知 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 斜率为
斜率为 的直线
的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于 两点,过
两点,过 且与
且与 垂直的直线
垂直的直线 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于 两点。
两点。
(1)求 的取值范围;
的取值范围;
求四边形 面积的最小值。
面积的最小值。