(本小题满分16分)定义在R上的函数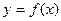 ,
, ,当
,当 时,
时, ,且
,且
对任意的 ∈R,有
∈R,有 .
.
(1)求证: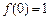 ;
;
(2)求证: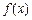 是R上的增函数;
是R上的增函数;
(3)若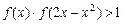 ,求
,求 的取值范围.
的取值范围.
为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本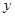 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为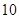 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴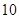 万元.
万元.
(1)当 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
如图,几何体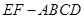 中,
中, 为边长为
为边长为 的正方形,
的正方形,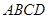 为直角梯形,
为直角梯形,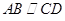 ,
, ,
, ,
,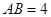 ,
,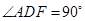 .
.
(1)求异面直线 和
和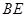 所成角的大小;
所成角的大小;
(2)求几何体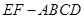 的体积.
的体积.
在△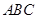 中,角
中,角 、
、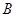 、
、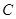 所对的边长分别为
所对的边长分别为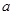 、
、 、
、 ,
,
且 .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)若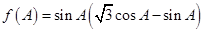 ,求
,求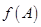 的取值范围.
的取值范围.
已知曲线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是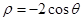 .
.
(1)写出 的极坐标方程和
的极坐标方程和 的直角坐标方程;
的直角坐标方程;
(2)已知点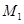 、
、 的极坐标分别是
的极坐标分别是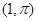 、
、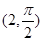 ,直线
,直线 与曲线
与曲线 相交于
相交于 、
、 两点,射线
两点,射线 与曲线
与曲线 相交于点
相交于点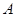 ,射线
,射线 与曲线
与曲线 相交于点
相交于点 ,求
,求 的值.
的值.
如图: 是⊙
是⊙ 的直径,
的直径,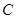 是弧
是弧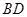 的中点,
的中点, ⊥
⊥ ,垂足为
,垂足为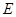 ,
,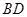 交
交 于点
于点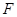 .
.
(1)求证: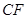 =
= ;
;
(2)若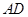 =4,⊙
=4,⊙ 的半径为6,求
的半径为6,求 的长.
的长.