如图: 是⊙
是⊙ 的直径,
的直径,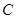 是弧
是弧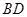 的中点,
的中点, ⊥
⊥ ,垂足为
,垂足为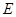 ,
,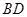 交
交 于点
于点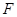 .
.
(1)求证: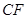 =
= ;
;
(2)若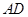 =4,⊙
=4,⊙ 的半径为6,求
的半径为6,求 的长.
的长.
下面给出的正多边形的边长都是20cm,请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.


图1图2图3
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,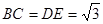 ,
,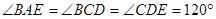
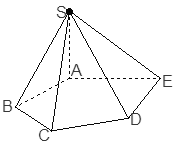
(1)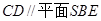 .
.
(2)证明:平面SBC⊥平面SAB.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=
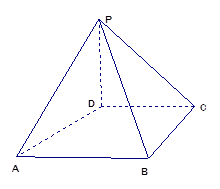
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离
四棱锥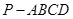 中,底面
中,底面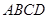 是
是 的菱形,侧面
的菱形,侧面 为正三角形.
为正三角形.
(1) .
.
(2)若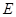 为
为 边的中点,过三点
边的中点,过三点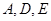 的平面交
的平面交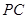 于点
于点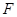 ,证明:
,证明: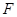 为
为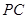 的中点.
的中点.
如图,在四面体 中,
中,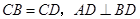 ,点
,点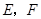 分别是
分别是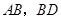 的中点.
的中点.
求证:(1)直线 面
面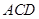 ;
;
(2)平面 面
面 .
.