(本小题满分12分)
如图1,在三棱锥P-A.BC中,PA.⊥平面A.BC,A.C⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.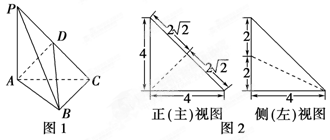
(1) 证明:A.D⊥平面PBC;
(2) 求三棱锥D-A.BC的体积;
(3) 在∠A.CB的平分线上确定一点Q,使得PQ∥平面A.BD,并求此时PQ的长.
(本小题满分12分)
已知函数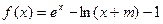 ,若x=0,函数f(x)取得极值
,若x=0,函数f(x)取得极值
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)已知a>b≥0,证明: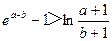 .
.
(本小题满分12分)已知直线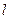 与抛物线
与抛物线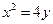 相切于点P(2,1),且与
相切于点P(2,1),且与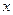 轴交于点A,定点B的坐标为(2,0)。
轴交于点A,定点B的坐标为(2,0)。
(I)若动点M满足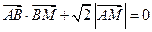 ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线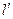 (斜率不等于零)与(I)中的轨迹C交于不同的两点E.F(E在B.F之间),试求
(斜率不等于零)与(I)中的轨迹C交于不同的两点E.F(E在B.F之间),试求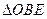 与
与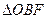 面积之比的取值范围。
面积之比的取值范围。
(本小题满分12分)
数列{an}的前n项和为Sn,且a1=a,Sn+1=2Sn+n+1,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)当a=1时,若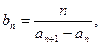 设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
设数列{bn}的前n项和Tn,n∈N*,证明Tn<2。
(本小题满分12分)
如图,在正三棱柱ABC—A1B1C1中,BB1=2,BC=2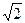 ,D为B1C1的中点。
,D为B1C1的中点。
(Ⅰ)证明:B1C⊥面A1BD;
(Ⅱ)求二面角B—AC—B1的大小。
(本小题满分12分)
某大学毕业生响应国家号召,到某村参加村委会主任应聘考核。考核依次分为笔试、面
试.试用共三轮进行,规定只有通过前一轮考核才能进入下一轮考核,否则将被淘汰,
三轮考核都通过才能被正式录用。设该大学毕业生通过三轮考核的概率分别为 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
(Ⅰ)求该大学毕业生未进入第三轮考核的概率;
(Ⅱ)设该大学毕业生在应聘考核中考核次数为ξ,求ξ的数学期望和方差。