某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为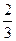 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为 ,求
,求 的分布列与均值E
的分布列与均值E .
.
已知函数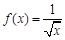 的定义域为集合
的定义域为集合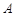 ,集合
,集合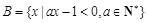 ,
,
集合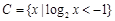 .
.
(1)求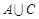 ;
;
(2)若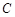
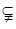 (
(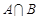 ),求
),求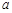 的值.
的值.
已知椭圆 :
: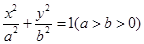 经过如下五个点中的三个点:
经过如下五个点中的三个点: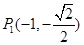 ,
,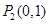 ,
,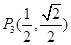 ,
,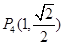 ,
,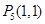 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设点 为椭圆
为椭圆 的左顶点,
的左顶点,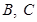 为椭圆
为椭圆 上不同于点
上不同于点 的两点,若原点在
的两点,若原点在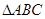 的外部,且
的外部,且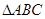 为直角三角形,求
为直角三角形,求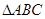 面积的最大值.
面积的最大值.
如图,在四棱锥 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, ,
, ,且
,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)棱 上是否存在一点
上是否存在一点 ,使直线
,使直线 与平面
与平面 所成的角是
所成的角是 ?若存在,求
?若存在,求 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
已知椭圆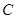 :
: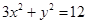 ,直线
,直线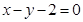 交椭圆
交椭圆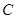 于
于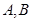 两点.
两点.
(Ⅰ)求椭圆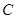 的焦点坐标及长轴长;
的焦点坐标及长轴长;
(Ⅱ)求以线段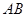 为直径的圆的方程.
为直径的圆的方程.
在平面直角坐标系 中,已知点
中,已知点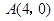 ,动点
,动点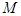 在
在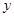 轴上的正射影为点
轴上的正射影为点 ,且满足直线
,且满足直线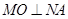 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)当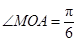 时,求直线
时,求直线 的方程.
的方程.