（本小题满分10分）2010年3月国家要求一些企业必须停业处理排污问题，于是各企业考虑引进污水处理设备，现有甲、乙两套设备可以引进。每个企业可引进一套，引进两套或都不引进自行研发。对于每个企业，甲被引进的概率为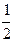
，乙被引进的概率为
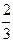，甲乙两套设备是否被引进相互独立，各企业之间是否引进也是相互独立的。
（Ⅰ）求A企业引进污水处理设备的概率；
（Ⅱ）记X表示3个企业中引进污水处理设备的企业个数，求X的分布列及期望。
已知函数
（
）的最小正周期为
．
（Ⅰ）求
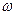的值；
（Ⅱ）求函数
在区间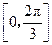
上的取值范围．
新课标要求学生数学模块学分认定由模块成绩决定，模块成绩由模块考试成绩和平时成绩构成，各占50%，若模块成绩大于或等于60分，获得2学分，否则不能获得学分（为0分），设计一算法，通过考试成绩和平时成绩计算学分，并画出程序框图。
已知直线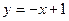
与椭圆
相交于A、B两点，且线段AB的中点，在直线
上.（1）求此椭圆的离心率；（2）若椭圆的右焦点关于直线
的对称点的在圆
上，求此椭圆的方程.
同时抛掷甲、乙两颗质地均匀的骰子（六个面上分别刻有1，2，3，4，5，6六个数字的正方体）。
（1）若甲上的数字为十位数，乙上的数字为个位数，问可以组成多少个不同的数，其中个位数字与十位数字均相同的数字的概率是多少?
（2）两个玩具的数字之和共有多少种不同结果?其中数字之和为12的有多少种情况?数字之和为6的共有多少种情况?分别计算这两种情况的概率。
某工厂用7万元钱购买了一台新机器，运输安装费用2千元，每年投保、动力消耗的费用也为2千元，每年的保养、维修、更换易损零件的费用逐年增加，第一年为2千元，第二年为3千元，第三年为4千元，依此类推，即每年增加1千元．问这台机器最佳使用年限是多少年？并求出年平均费用的最小值．