(本小题满分10分)求下列函数的导函数:
(1)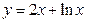 (2)
(2)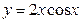 (3)
(3)
已知函数 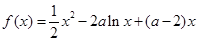 ,
,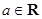 .
.
(Ⅰ)当  时,求函数
时,求函数  的最小值; (Ⅱ)当
的最小值; (Ⅱ)当 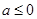 时,讨论函数
时,讨论函数  的单调性;
的单调性;
(Ⅲ)是否存在实数 ,对任意的
,对任意的  ,且
,且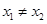 ,有
,有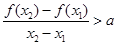 ,恒成立,若存在求出
,恒成立,若存在求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
如图,在四棱锥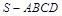 中,平面
中,平面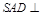 平面
平面 .底面
.底面 为矩形,
为矩形, 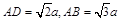 ,
,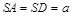 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角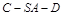 的大小.
的大小.
数列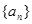 的前
的前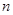 项和记为
项和记为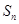 ,
, ,点
,点 在直线
在直线 上,
上, .
.
(Ⅰ)当实数 为何值时,数列
为何值时,数列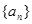 是等比数列?
是等比数列?
(Ⅱ)在(Ⅰ)的结论下,设 ,
,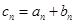 ,
, 是数列
是数列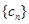 的前
的前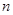 项和,求
项和,求 。
。
如图,在△ABC中,已知B=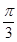 ,AC=4
,AC=4 ,D为BC边上一点.
,D为BC边上一点.
(I)若AD=2,S△ABC=2 ,求DC的长;
,求DC的长;
(Ⅱ)若AB=AD,试求△ADC的周长的最大值.
(本小题满分14分)
已知函数f(x)= x
x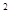 -ax + (a-1)
-ax + (a-1)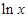 ,
,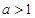 .
.
(I)讨论函数 的单调性;
的单调性;
(II)若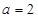 ,数列
,数列 满足
满足 .
.
若首项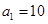 ,证明数列
,证明数列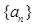 为递增数列;
为递增数列;
若首项为正整数,数列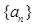 递增,求首项的最小值.
递增,求首项的最小值.