(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,已知AB = 3,AD = 2,PA = 2,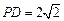 ,
, .
.
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P—BD—A的大小.
已知 ,
, 比较下列各题中两个代数式值的大小:
比较下列各题中两个代数式值的大小:
(1) 与
与 ;
;
(2) 与
与 .
.
已知椭圆 的方程为
的方程为 ,点
,点 分别为其左、右顶点,点
分别为其左、右顶点,点 分别为其左、右焦点,以点
分别为其左、右焦点,以点 为圆心,
为圆心, 为半径作圆
为半径作圆 ;以点
;以点 为圆心,
为圆心, 为半径作圆
为半径作圆 ;若直线
;若直线 被圆
被圆 和圆
和圆 截得的弦长之比为
截得的弦长之比为 ;
;
(1)求椭圆 的离心率;
的离心率;
(2)己知 ,问是否存在点
,问是否存在点 ,使得过
,使得过 点有无数条直线被圆
点有无数条直线被圆 和圆
和圆 截得的弦长之比为
截得的弦长之比为 ;若存在,请求出所有的
;若存在,请求出所有的 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
已知椭圆 的离心率为
的离心率为 ,过右顶点
,过右顶点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,且
两点,且 .
.
(1)求椭圆 和直线
和直线 的方程;
的方程;
(2)记曲线 在直线
在直线 下方的部分与线段AB所围成的平面区域(含边界)为
下方的部分与线段AB所围成的平面区域(含边界)为 .若曲线
.若曲线 与
与 有公共点,试求实数
有公共点,试求实数 的最小值.
的最小值.
已知舰 在舰
在舰 的正东,距离6公里,舰
的正东,距离6公里,舰 在舰
在舰 的北偏西30°,距离4公里,它们准备围找海洋动物,某时刻舰
的北偏西30°,距离4公里,它们准备围找海洋动物,某时刻舰 发现动物信号,4秒后,舰
发现动物信号,4秒后,舰 ,
, 同时发现这种信号,
同时发现这种信号, 于是发射麻醉炮弹,设舰与动物都是静止的,动物信号的传播速度为1公里/1秒,求舰
于是发射麻醉炮弹,设舰与动物都是静止的,动物信号的传播速度为1公里/1秒,求舰 炮击的方位角.
炮击的方位角.
已知抛物线方程为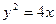 ,过点
,过点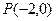 的直线AB交抛物线于点
的直线AB交抛物线于点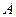 、
、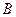 ,若线段
,若线段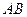 的垂直平分线交
的垂直平分线交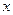 轴于点
轴于点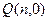 ,求
,求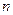 的取值范围.
的取值范围.