(本小题满分12分)某市十所重点中学进行高三联考,为了了解数学学科的考试情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表: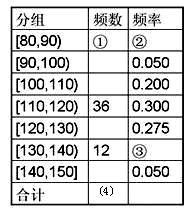

(1)根据上面频率分布表,求①,②,③,④处的数值;
(2)在所给的坐标系中画出区间 上的频率分布直方图;
上的频率分布直方图;
(3)从样本在 的个体中任意抽取
的个体中任意抽取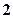 个个体,求至少有一个个体落在
个个体,求至少有一个个体落在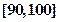 的概率。
的概率。
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD= .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,
试确定t的值
(本题满分14分) 已知数列 的首项
的首项
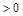 ,
, ,
,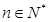
(1)若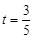 ,求证
,求证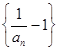 是等比数列并求出
是等比数列并求出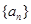 的通项公式;
的通项公式;
(2)若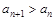 对一切
对一切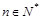 都成立,求
都成立,求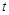 的取值范围。
的取值范围。
(本题满分14分) 已知角 的顶点在原点,始边与
的顶点在原点,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数 ,求函数
,求函数 在区间
在区间 上的取值范围.
上的取值范围.
(本题满分15分)
已知实数 满足
满足 且
且 ,设函数
,设函数
(Ⅰ) 当 时,求f (x)的极小值;
时,求f (x)的极小值;
(Ⅱ) 若函数 (
( )的极小值点与f (x)的极小值点相同.
)的极小值点与f (x)的极小值点相同.
求证:g(x)的极大值小于等于 .
.
(本题满分15分)
已知中心在原点O,焦点在x轴上,离心率为 的椭圆过点(
的椭圆过点( ,
, ).
).
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.