等数差列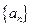 中,
中,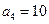 且
且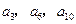 成等比数列,求数列
成等比数列,求数列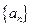 前20项的和
前20项的和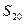 .
.
已知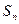 为数列
为数列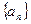 的前
的前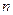 项和,求下列数列
项和,求下列数列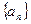 的通项公式:
的通项公式:
⑴ 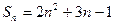 ;⑵
;⑵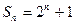 .
.
已知数列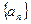 和
和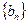 满足:
满足: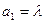 ,
, ,
,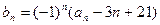 ,
,
其中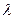 为实数,
为实数,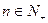 .
.
⑴ 对任意实数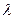 ,证明数列
,证明数列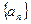 不是等比数列;
不是等比数列;
⑵ 证明:当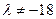 ,数列
,数列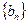 是等比数列;
是等比数列;
⑶设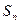 为数列
为数列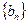 的前
的前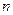 项和,是否存在实数
项和,是否存在实数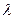 ,使得对任意正整数
,使得对任意正整数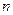 ,都有
,都有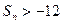 ?
?
若存在,求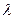 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本小题共16分)设函数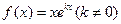 .
.
(Ⅰ)求曲线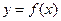 在点
在点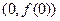 处的切线方程;(Ⅱ)求函数
处的切线方程;(Ⅱ)求函数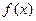 的单调区间;
的单调区间;

(Ⅲ)若函数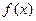 在区间
在区间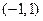 内单调递增,求
内单调递增,求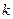 的取值范围.
的取值范围.
|
已知函数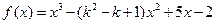 ,
,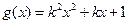 ,
,
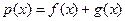 .若
.若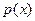 在区间
在区间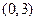 上不单调,求
上不单调,求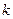 的取值范围;
的取值范围;
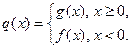 是否存在
是否存在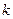 ,对任意给定的非零实数
,对任意给定的非零实数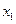 ,存在惟一的非零实数
,存在惟一的非零实数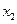 (
(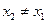 ),使得
),使得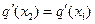 成立?若存在,求
成立?若存在,求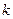 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.