(12分)某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率;
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率;
(3)求该同学获得奖金 的数学期望(精确到元).
的数学期望(精确到元).
(本小题满分13分)
已知函数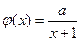 ,
,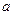 为正常数.
为正常数.
(1)若 ,且
,且 ,求函数
,求函数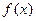 的单调增区间;
的单调增区间;
(2)若 ,且对任意
,且对任意 ,
,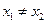 ,都有
,都有 ,求
,求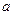 的的取值范围.
的的取值范围.
(本小题满分13分)
给定椭圆 >
> >0
>0 ,称圆心在原点
,称圆心在原点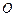 ,半径为
,半径为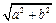 的圆是椭圆
的圆是椭圆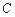 的“准圆”
的“准圆” 。若椭圆
。若椭圆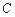 的一个焦点为
的一个焦点为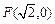 ,其短轴上的一个端点到
,其短轴上的一个端点到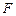 的距离为
的距离为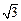 。
。
(1)求椭圆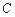 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点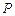 是椭圆
是椭圆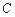 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点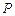 作直线
作直线 ,使得
,使得 与椭圆
与椭圆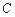 都只有一个交点。求证:
都只有一个交点。求证: ⊥
⊥ .
.
(本小题满分13分)
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
(本小题满分12分)
已知正方形ABCD的边长为1,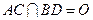 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线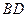 折起,使
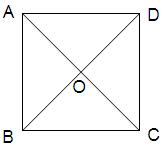
折起,使 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.
(1)求证: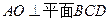 ;
;
(2)求二面角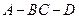 的余弦值.
的余弦值.
 |
|||||
 |
|||||
 |
|||||
(本 小题满分12分)
小题满分12分)
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别
从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为 ,“实用性”得分为
,“实用性”得分为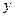 ,统计结果如下表:
,统计结果如下表:
 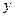 作品数量  |
实用性 |
|||||
| 1分 |
2分 |
3分 |
4分 |
5分 |
||
创 新 性 |
1分 |
1 |
3 |
1 |
0 |
1 |
| 2分 |
1 |
0 |
7 |
5 |
1 |
|
| 3分 |
2 |
1 |
0 |
9 |
3 |
|
| 4分 |
1 |
 |
6 |
0 |
 |
|
| 5分 |
0 |
0 |
1 |
1 |
3 |
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为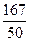 ,求
,求 、
、 的值.
的值.