如下图所示,在直角坐标系 中,射线
中,射线 在第一象限,且与
在第一象限,且与 轴的正半轴成定角
轴的正半轴成定角 ,动点
,动点 在射线
在射线 上运动,动点
上运动,动点 在
在 轴的正半轴上运动,
轴的正半轴上运动, 的面积为
的面积为 .
.
(Ⅰ)求线段 中点
中点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ) 是曲线
是曲线 上的动点,
上的动点,  到
到 轴的距离之和为
轴的距离之和为 ,
,
设 为
为 到
到 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数 ,
,
使 恒成立?若存在,求出这个
恒成立?若存在,求出这个 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数 ,函数
,函数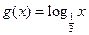 .
.
(1)若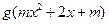 的值域为
的值域为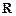 ,求实数
,求实数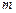 的取值范围;
的取值范围;
(2)当 时,求函数
时,求函数 的最小值
的最小值 ;
;
(3)是否存在非负实数m、n,使得函数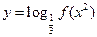 的定义域为
的定义域为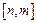 ,值域为
,值域为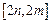 ,
,
若存在,求出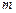 、
、 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
已知函数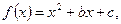 且
且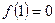 .
.
(1)若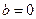 ,求函数
,求函数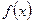 在区间
在区间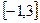 上的最大值和最小值;
上的最大值和最小值;
(2)要使函数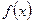 在区间
在区间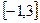 上单调递增,求
上单调递增,求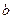 的取值范围.
的取值范围.
已知全集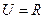 ,
, 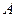 =
=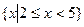 ,集合
,集合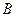 是函数
是函数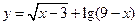 的定义域.
的定义域.
(1)求集合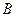 ;
;
(2)求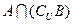 .
.
已知函数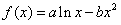 图象上一点
图象上一点 处的切线方程为
处的切线方程为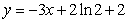 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若方程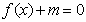 在
在 内有两个不等实根,求
内有两个不等实根,求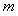 的取值范围(其中
的取值范围(其中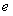 为自然对数的底数);
为自然对数的底数);
(Ⅲ)令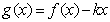 ,若
,若 的图象与
的图象与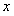 轴交于
轴交于 ,
,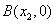 (其中
(其中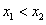 ),
),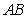 的中点为
的中点为 ,求证:
,求证: 在
在 处的导数
处的导数 .
.