(本小题满分14分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为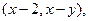 记
记 .
.
(1)求随机变量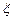 的
的 最大值,并求事件“
最大值,并求事件“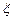 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量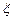 的分布列和数学期望.
的分布列和数学期望.
在 ABC中,内角A,B,C的对边
ABC中,内角A,B,C的对边 分别为a,b,c.已知
分别为a,b,c.已知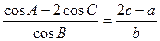 .
.
(I)求 的值;
的值;
(II)若cosB= ,b=2,求△ABC的面积S。
,b=2,求△ABC的面积S。
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(已知sin41°
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(已知sin41°
 ,角度精确到1
,角度精确到1 )?
)?
已知{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,
(1)求数列{an}的首项a1及公差为d
(2)证明:数列{ }为等差数列并求其前n项和Tn
}为等差数列并求其前n项和Tn 。
。
在△ABC中,已知a=2 ,b=6,A=30°,解三角形.
,b=6,A=30°,解三角形.
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数 是一个随机变量,它的分布列为:
是一个随机变量,它的分布列为: ;设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大?
;设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元. 问电器商每月初购进多少台电冰箱才能使月平均收益最大?