（本小题满分12分）某学校高一、高二、高三的三个年级学生人数如下表
| |
高三 |
高二 |
高一 |
| 女生 |
100 |
150 |
z |
| 男生 |
300 |
450 |
600 |
按年级分层抽样的方法评选优秀学生50人，其中高三有10人．
（1）求z的值；
（2）用分层抽样的方法在高一中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2人，求至少有1名女生的概率；
（3）用随机抽样的方法从高二女生中抽取8人,经检测她们的得分如下：9．4，8．6，9．2， 9．6，8．7，9．3
，9．0，8．2，把这8人的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0．5的概率．
在锐角
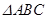中，角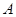
、
、
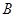所对的边分别为
、
、
.
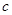且
.
（1）求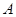角的大小及角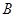的取值范围；
（2）若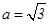
，求
的取值范围.
已知函数
（I）当a=0时，解不等式
；
（II）若存在x∈R，使得，f（x）≤g（x）成立，求实数a的取值范围．
在直角坐标系xoy中，圆C的参数方程为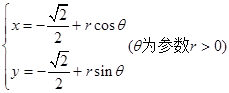
以O为极点，x轴的非负半轴为极轴，并取相同的长度单位建立极坐标系，直线l的极坐标方程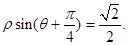
（I）求圆心的极坐标。
（II）若圆C上点到直线l的最大距离为3，求r的值。
如图，直线AB经过圆上O的点C，并且OA=OB，CA=CB，圆O交于直线OB于E，D，连接EC，CD，若tan∠CED=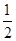
，圆O的半径为3，求OA的长．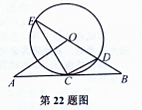
设函数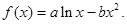
（I）若函数f（x）在x=1处与直线y=
相切，
①求实数a，b的值；
②求函数f（x）在[
土，e]上的最大值．
（II）当b=0时，若不等式f（x）≥m+x对所有的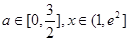
都成立，求实数m的取值范围，