18.(本小题满分14分)
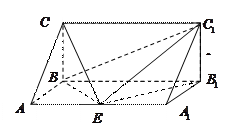
一个三棱柱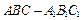 直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设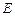 、
、 分别为
分别为 和
和 的中点.
的中点.
(Ⅰ)求几何体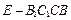 的体积;
的体积;
(Ⅱ)证明: 平面
平面 ;
;
(Ⅲ)证明:平面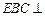 平面
平面 .
.
(本小题满分12分)
已知数列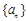 的前n项和为
的前n项和为 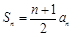 (n∈N*),且
(n∈N*),且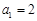 .数列
.数列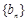 满足
满足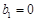 ,
,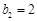 ,
,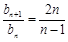 ,n=2,3,….
,n=2,3,….
(Ⅰ)求数列 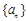 的通项公式;
的通项公式;
(Ⅱ)求数列 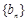 的通项公式;
的通项公式;
(Ⅲ)证明:对于  ,
,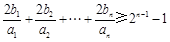 .
.
(本小题满分12分)
如图,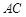 是圆
是圆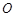 的直径,点
的直径,点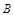 在圆
在圆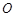 上,
上, ,
,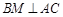 交
交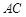 于点
于点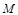 ,
,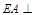 平面
平面 ,
, ,
,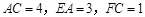 .
.
(1)证明: ;
;
(2)求平面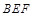 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题满分12分)
某汽车配件厂生产A、B两种型号的产品,A型产品的一等品率为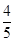 ,二等品率为
,二等品率为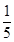 ;B型产品的一等品率为
;B型产品的一等品率为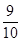 ,二等品率为
,二等品率为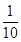 。生产1件A型产品,若是一等品则获得4万元利润,若是二等品则亏损1万元;生产1件B型产品,若是一等品则获得6万元利润,若是二等品则亏损2万元。设生产各件产品相互独立。
。生产1件A型产品,若是一等品则获得4万元利润,若是二等品则亏损1万元;生产1件B型产品,若是一等品则获得6万元利润,若是二等品则亏损2万元。设生产各件产品相互独立。
(1)求生产4件A型产品所获得的利润不少于10万元的概率;
(2)记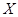 (单位:万元)为生产1件A型产品和1件B型产品可获得的利润,求
(单位:万元)为生产1件A型产品和1件B型产品可获得的利润,求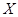 的分布列及期望值.
的分布列及期望值.
(本小题满分12分)
已知 中,角
中,角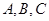 的对边分别为
的对边分别为 ,
, 且
且 的面积
的面积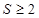 ,
,
(1)求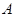 的取值范围;
的取值范围;
(2)求函数 的最值.
的最值.
(本小题满分12分)
已知函数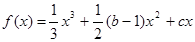 (b、c为常数).
(b、c为常数).
(1) 若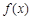 在
在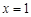 和
和 处取得极值,试求b,c的值;
处取得极值,试求b,c的值;
(3)若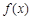 在
在 、
、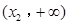 上单调递增,且在
上单调递增,且在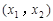 上单调递减,又满足
上单调递减,又满足 ,求证:
,求证: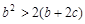 .
.