如图所示，
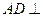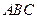平面
，
平面，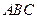
，
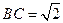，凸多面体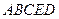
的体积为
，
为
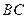的中点．
（Ⅰ）求证：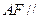
平面
；
（Ⅱ）求证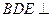：平面
平面
．
(本小题满分12分)
为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
| 睡眠时间(小时) |
 |
 |
 |
 |
 |
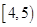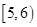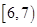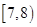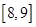| 人数 |
 |
 |
 |
|
|
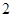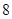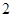男生:
| 睡眠时间(小时) |
|
|
|
|
|
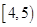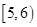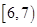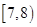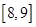| 人数 |
 |
 |
 |
|
 |
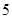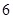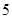（1）现把睡眠时间不足5小时的定义为“严重睡眠不足”，从睡眠时间不足6小时的女生中随机抽取3人，求此3人中恰有一人为“严重睡眠不足”的概率;
（2）完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”？
| 睡眠时间少于7小时 |
睡眠时间不少于7小时 |
合计 |
|
| 男生 |
|||
| 女生 |
|||
| 合计 |
（
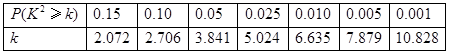
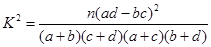，其中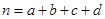
）
(本小题满分12分)
已知等差数列
的前
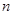项和为
,
,
.
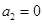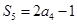（1）求数列的通项公式;
（2）设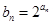
,求数列
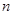的前项和为
.
(本小题满分10分) 选修4—5：不等式选讲.
已知函数
.
（1）若不等式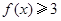
恒成立,求
的取值范围;
（2）当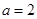
时,求不等式
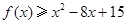的解集.
(本小题满分10分) 选修4—4：坐标系与参数方程.
已知曲线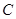
的参数方程为
（
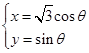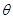为参数）,直线
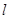的极坐标方程为
.
（1）写出曲线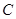的普通方程和直线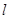的直角坐标方程;
（2）设点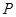
为曲线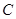上的动点,求点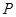到直线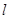距离的最大值.
(本小题满分10分) 选修4—1：几何证明选讲.
已知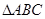
中, 
,以点
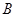为圆心,以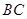
为半径的圆分别交
,
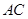于两
,
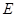两点,且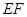
为该圆的直径.
（1）求证: 
;
（2）若
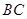.求的长.