(本小题满分13分)
已知数列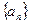 中,
中, 且点
且点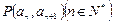 在直线
在直线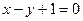 上。
上。
(1)求数列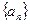 的通项公式;
的通项公式; (2)若函数
(2)若函数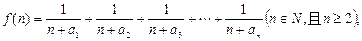 求函数
求函数 的最小值;
的最小值;
(3)设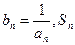 表示数列
表示数列 的前
的前 项和。试问:是否存在关于
项和。试问:是否存在关于 的整式
的整式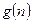 ,使得
,使得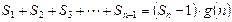 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出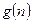 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
(本小题满分10分)已知函数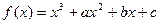 的图象过原点,且
的图象过原点,且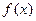 在
在 、
、 处取得极值.
处取得极值.
(Ⅰ)求函数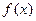 的单调区间及极值;
的单调区间及极值;
(Ⅱ)若函数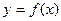 与
与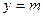 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.
(本小题满分10分)已知 ,
, , 且
, 且
(1) 求函数 的解析式;
的解析式;
(2) 当 时,
时,  的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 并求出相应的
的最大值, 并求出相应的 的值.
的值.
(本小题满分10分)某港口的水深 (米)是时间
(米)是时间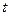 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
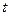 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,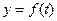 可近似的看成是函数
可近似的看成是函数
(1)根据以上数据,求出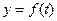 的解析式
的解析式
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
(本小题满分8分)已知 ,
, ,当
,当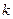 为何值时,
为何值时,
(1)  与
与 垂直?
垂直?
(2)  与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(满分8分)已知的值.