(本小题满分10分)某港口的水深 (米)是时间
(米)是时间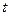 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
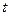 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,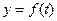 可近似的看成是函数
可近似的看成是函数
(1)根据以上数据,求出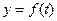 的解析式
的解析式
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
.某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 |
58 |
53 |
87 |
62 |
78 |
70 |
82 |
| 第二次被抽到进行检验的技术员 |
64 |
61 |
78 |
66 |
74 |
71 |
76 |
①求先后被选出的两名技术员中恰有一名女技术员的概率;
②请问哪位技术员检验更稳定?并说明理由.
三、解答题(本大题有5道小题,各小题12分,共60分)
17.在 中,
中,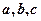 分别是角
分别是角 的对边,向量
的对边,向量 ,
,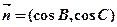 ,且
,且 .
.
(1)求角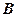 的大小;
的大小;
(2)设 ,且
,且 的最小正周期为
的最小正周期为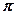 ,求
,求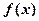 在
在
区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
已知函数
(1)求函数的定义域,并证明 在定义域上是奇函数;
在定义域上是奇函数;
(2)对于
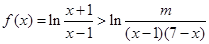 恒成立,求实数
恒成立,求实数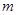 的取值范围;
的取值范围;
、(本小题满分12分)
已知等差数列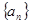 的公差大于0,且
的公差大于0,且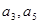 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且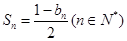 .
.
(1)求数列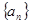 ,
, 的通项公式;
的通项公式;
(2)若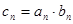 求数列
求数列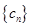 的前
的前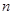 项和
项和 .
.
(本小题满分12分)
在正三棱柱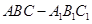 中,底面边长和侧棱都是2,D是侧棱
中,底面边长和侧棱都是2,D是侧棱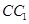 上任意一点.E是
上任意一点.E是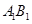 的中点.
的中点.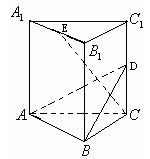
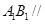 (1)求证:平面ABD;
(1)求证:平面ABD;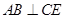 (2)求证:;
(2)求证:;
(3)求三棱锥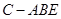 的体积。
的体积。