对于定义域为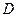 的函数
的函数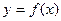 ,若同时满足下列条件:
,若同时满足下列条件:
① 在
在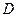 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间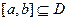 ,使
,使 在
在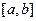 上的值域为
上的值域为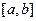 ;那么把
;那么把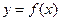
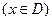 叫闭函数.
叫闭函数.
(1)求闭函数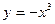 符合条件②的区间
符合条件②的区间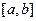 ;
;
(2)判断函数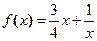 ,
,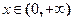 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若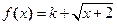 是闭函数,求实数
是闭函数,求实数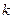 的范围?
的范围?
(本小题满分12分)已知:以点 为圆心的圆与x轴交于
为圆心的圆与x轴交于
点O,A,与y轴交于点O,B,其中O为原点。
(Ⅰ) 求证:⊿OAB的面积为定值;
(Ⅱ) 设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程。
(本小题满分12分)一个圆锥高h为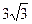 ,侧面展开图是个半圆,求:
,侧面展开图是个半圆,求:
(1)其母线l与底面半径r之比;
(2)锥角 ;
;
(3)圆锥的表面积
已知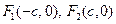 是椭圆
是椭圆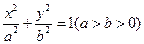 的左、右焦点,过点
的左、右焦点,过点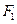 作
作
倾斜角为 的直线
的直线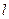 交椭圆于
交椭圆于 两点,
两点, .
.
(1)求椭圆的离心率;
(2)若 ,求椭圆的标准方程.
,求椭圆的标准方程.
已知函数 的图象经过点
的图象经过点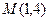 ,曲线在点
,曲线在点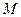 处的切线恰好与
处的切线恰好与
直线 垂直.
垂直.
(1)求实数 的值;
的值;
(2)若函数 在区间
在区间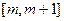 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
已知函数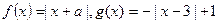 .
.
(1)解关于 的不等式
的不等式 ;
;
(2)若对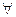
 ,
,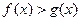 恒成立,求
恒成立,求 的取值范围.
的取值范围.