已知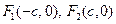 是椭圆
是椭圆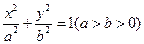 的左、右焦点,过点
的左、右焦点,过点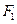 作
作
倾斜角为 的直线
的直线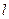 交椭圆于
交椭圆于 两点,
两点, .
.
(1)求椭圆的离心率;
(2)若 ,求椭圆的标准方程.
,求椭圆的标准方程.
(本小题满分12分)
某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生,
其中8名女生中有3名报考理科,男生中有2名报考文科
(1)是根据以上信息,写出 列联表
列联表
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?参考公式
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
 |
2.07 |
2.71 |
3.84 |
5.02 |
6.64 |
7.88 |
10.83 |
(本小题满分12分)若复数
(1)若 在复平面内对应的点
在复平面内对应的点 在第二象限内,求
在第二象限内,求 的取值范围.
的取值范围.
(2)若 为纯虚数时,求
为纯虚数时,求 .
.
已知函数 ,
,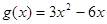 ,又函数
,又函数 在
在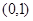 单调递减,而在
单调递减,而在 单调递增.
单调递增.
(1)求 的值;
的值;
(2)求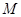 的最小值,使对
的最小值,使对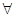
 ,有
,有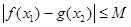 成立;
成立;
(3)是否存在正实数 ,使得
,使得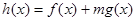 在
在 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
已知 .经计算得
.经计算得 ,
,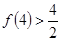 ,
, ,
,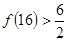 ,
, ,通过观察,我们可以得到一个一般性的结论.
,通过观察,我们可以得到一个一般性的结论.
(1)试写出这个一般性的结论;
(2)请用数学归纳法证明这个一般性的结论;
(3)对任一给定的正整数 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得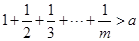 ?
?
若存在,请给出符合条件的正整数 的一个值;若不存在,请说明理由.
的一个值;若不存在,请说明理由.
阅读下面材料:
根据两角和与差的正弦公式,有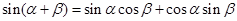 ------①
------①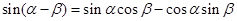 ------②
------②
由①+② 得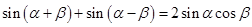 ------③
------③
令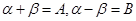 有
有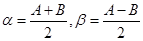
代入③得 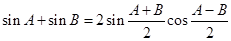 .
.
(1) 类比上述推理方法,根据两角和与差的余弦公式,证明: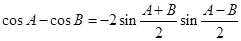 ;
;
(2)若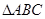 的三个内角
的三个内角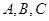 满足
满足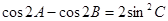 ,直接利用阅读材料及(1)中的结论试判断
,直接利用阅读材料及(1)中的结论试判断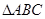 的形状.
的形状.