已知椭圆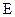 的中心是坐标原点,焦点在坐标轴上,且椭圆过点
的中心是坐标原点,焦点在坐标轴上,且椭圆过点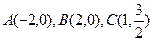 三点.
三点.
(1)求椭圆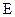 的方程;
的方程;
(2)若点 为椭圆
为椭圆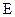 上不同于
上不同于 的任意一点,
的任意一点, ,求
,求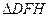 内切圆的面积的最大值,并指出其内切圆圆心的坐标.
内切圆的面积的最大值,并指出其内切圆圆心的坐标.
已知抛物线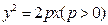 的焦点为
的焦点为 是抛物线上横坐标为
是抛物线上横坐标为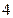 ,且位于
,且位于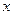 轴上方的点,
轴上方的点, 到抛物线准线的距离等于
到抛物线准线的距离等于 .过
.过 作
作 垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为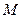 .
.
(1)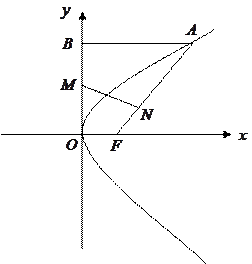 求抛物线方程;
求抛物线方程;
(2)过 作
作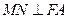 ,垂足为
,垂足为 ,求点
,求点 的坐标;
的坐标;
(3)以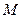 为圆心,
为圆心, 为半径作圆
为半径作圆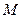 .当
.当 是
是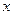 轴上一动点
轴上一动点
时,讨论直线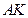 与圆
与圆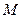 的位置关系.
的位置关系.
已知双曲线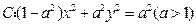 ,若
,若 的上支顶点为
的上支顶点为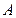 ,且上支与直线
,且上支与直线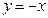 交于点
交于点 ,以
,以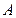 为焦点,
为焦点,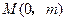 为顶点,开口向下的抛物线通过点
为顶点,开口向下的抛物线通过点 ,当
,当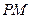 的斜率
的斜率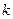 在区间
在区间 上变化时,求实数
上变化时,求实数 的取值范围.
的取值范围.
设抛物线 的准线与
的准线与 轴的交点为
轴的交点为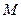 ,过点
,过点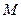 作直线
作直线 交抛物线于
交抛物线于 两点.若直线
两点.若直线 的斜率依次取
的斜率依次取 时,线段
时,线段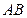 的垂直平分线与对称轴的交点依次为
的垂直平分线与对称轴的交点依次为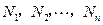 ,当
,当 时,求
时,求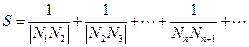 的值.
的值.
设抛物线 的准线与
的准线与 轴的交点为
轴的交点为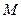 ,过点
,过点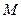 作直线
作直线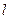 交抛物线于
交抛物线于 两点,若线段
两点,若线段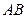 的垂直平分线交对称轴于
的垂直平分线交对称轴于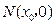 ,求证:
,求证: ;
;
设抛物线 的准线与
的准线与 轴的交点为
轴的交点为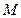 ,过点
,过点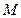 作直线
作直线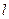 交抛物线于
交抛物线于 两点.
两点.
求线段 中点的轨迹方程;
中点的轨迹方程;