某化妆品生产企业为了占有更多的市场份额,拟在2010年世博会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量 万件与年促销费
万件与年促销费 万元之间满足
万元之间满足 与
与 成反比例,如果不搞促销活动,化妆品的年销量只能是l万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产l万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完。
成反比例,如果不搞促销活动,化妆品的年销量只能是l万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产l万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完。
 (1)将2010年的利润
(1)将2010年的利润 (万元)表示为促销费
(万元)表示为促销费 (万元)的函数;
(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
如图,直线l与⊙O相切于点A,点P为直线l上一点,直线PO交⊙O于点C、B,点D在线段AP上,连结DB,且AD=DB.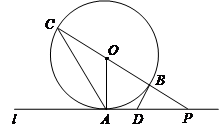
 (1)判断直线DB与⊙O的位置关系,并说明理由;
(1)判断直线DB与⊙O的位置关系,并说明理由;
(2)若PB=BO,⊙O的半径为4cm,求AC的长.
如图,已知正比例函数y=2x的图像l1与反比例函数y= 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
(1)求反比例函数的解析式;
(2)求△DOB的面积.
如图,已知点M在菱形ABCD的BC边上,连结AM交BD于点E,过菱形ABCD的顶点C作CN∥AM,分别交BD、AD于点F、N,连结AF、CE.判断四边形AECF的形状,并说明理由.
解不等式(组)
(1)
(2)
解方程(组):
(1)
(2)