某项考试按科目
、科目
依次进行，只有当科目成绩合格时，才可以继续参加科目 的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目成绩合格的概率均为
，每次考科目成绩合格的概率均为
。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试
的次数为
。
(1)求的分布列和均值；
(2)求该同学在这项考试中获得合格证书的概率。
已知函数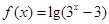
，
（1）求函数
的定义域和值域；
（2）设函数
，若不等式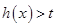
无解，求实数
的取值范围．
某企业常年生产一种出口产品，根据预测可知，进入2l世纪以来，该产品的产量平稳增长．记2008年为第1年，且前4年中，第
年与年产量
（万件）之间的关系如下表所示：
|
1 |
2 |
3 |
4 |
|
4.00 |
5.58 |
7.00 |
8.44 |
若近似符合以下三种函数模型之一：
．
（1）找出你认为最适合的函数模型，并说明理由，然后选取08年和10年的数据求出相应的解析式；
（2）因遭受某国对该产品进行反倾销的影响，2014年的年产量比预计减少30％，试根据所建立的函数模型，确定2014年的年产量．
已知函数
的图像过点
（1）求实数
的值及
的周期及单调递增区间；
（2）若
，求的值域.
已知函数
的定义域为集合
，函数
的值域为集合
,
.
（1）求 
；
（2）若
且
,求实数
的取值范围,
设
的定义域为
，且在是递增的，
（1）求证：
；
（2）设
，解不等式
．