（本小题满分14分）（注意：在试题卷上作答无效）设数列
的前
项和为
，对一切
，点
都在函数
的图象上．（Ⅰ）求
及数列的通项公式
； （Ⅱ）将数列依次按1项、2项、3项、4项循环地分为（
），（
，
），（
，
，
），（
，
，
，
）；（
），（
，
），（
，
，
），（
，
，
，
）；（
），…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为
，求
的值；
（Ⅲ）令
（
），求证：
．
（本题15分）已知方程x2+y2-2（m+3）x+2（1-4m2）y+16m4+9=0表示一个圆
（1）求实数m的取值范围；
（2）求该圆半径r的取值范围；
（3）求圆心的轨迹方程。
（本题15分）已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD．
（1）求证:PF⊥FD；
（2）设点G在PA上,且EG//平面PFD,试确定点G的位置．
在正方体ABCD-A1B1C1D1中, AA1=2,E为棱CC1的中点．
（1）求三棱锥E-ABD的体积；
（2）求证：B1D1
AE；
（3）求证：AC//平面B1DE．
（本题15分）如图，ABCD是正方形，O是正方形的中心，PO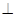
底面ABCD，E是PC的中点。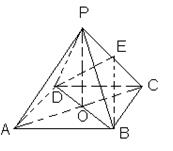
求证：（1）PA∥平面BDE
（2）平面PAC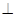平面BDE
（本题15分）根据下列条件，求圆的方程
（1）求经过两点
，且圆心在y轴上的圆的方程。
（2）圆的的半径为1，圆心与点（1，0）关于
对称的圆的方程。