(本小题满分15分)
已知圆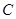 过定点
过定点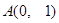 ,圆心
,圆心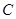 在抛物线
在抛物线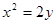 上,
上,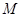 、
、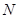 为圆
为圆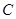 与
与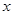 轴的交点.
轴的交点.
(1)当圆心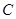 是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
(2)当圆心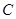 在抛物线上运动时,
在抛物线上运动时,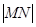 是否为一定值?请证明你的结论.
是否为一定值?请证明你的结论.
(3)当圆心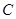 在抛物线上运动时,记
在抛物线上运动时,记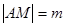 ,
,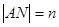 ,求
,求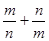 的最大值,并求出此时圆
的最大值,并求出此时圆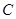 的方程.
的方程.
本题8分)
已知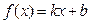 ,且
,且 ,
,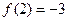 .
.
(1)求 解析式
解析式
(2)判断函数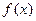 的单调性,并给予证明
的单调性,并给予证明
(本题8分)
已知集合 ,
,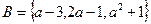
 ,若
,若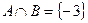 .
.
求实数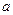 的值。
的值。
解不等式(本题共 8分)
8分)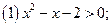
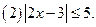
(本小题满分14分)已知函数 满足
满足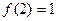 ,且
,且 有唯一实数解。
有唯一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记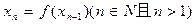 ,且
,且 =
=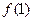 ,求数列
,求数列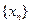 的通项公式。
的通项公式。
(3)记  ,数列{
,数列{ }的前
}的前 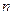 项和为
项和为 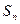 ,是否存在k∈N*,使得
,是否存在k∈N*,使得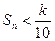 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
(本小题满分14分)某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元。
(1)若扣除投资及各种经费,则从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,按以下方案处理工厂:纯利润总和最大时,以16万美元出售该厂,问多长时间可以出售该工厂?能获利多少?