(本小题满分12分)已知单调递增的等比数列 满足:
满足: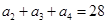 ,且
,且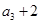 是
是 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)若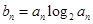 ,
, ,求
,求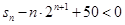 成立的正整数
成立的正整数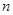 的最小值.
的最小值.
(本小题满分12分)某学校举行元旦晚会,组委会招募了12名男志愿者和18名 女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm),身高在175 cm以上(包括175 cm)定义为“高个子”,身高在175 cm以下(不包括175 cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率;
(2)若从身高180 cm以上(包括180 cm)的志愿者中选出男、女各一人,求这2人身高相差5 cm以上的概率.
(本小题满分12分)在 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
已知函数 ,
, ,其中
,其中 且
且 .
.
(1)判断函数 的单调性;
的单调性;
(2)当 时,求函数
时,求函数 在区间
在区间 上的最值;
上的最值;
(3)设函数 当
当 时,若对于任意的
时,若对于任意的 ,总存在唯一的
,总存在唯一的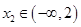 ,使得
,使得 成立,试求
成立,试求 的取值范围.
的取值范围.
已知函数 为常数.
为常数.
(1)当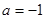 时,求
时,求 的单调区间;
的单调区间;
(2)当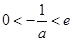 时,若
时,若 在区间
在区间 上的最大值为
上的最大值为 ,求
,求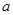 的值;
的值;
(3)当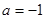 时,试推断方程
时,试推断方程 =
= 是否有实数解.
是否有实数解.