（本小题满分12分）
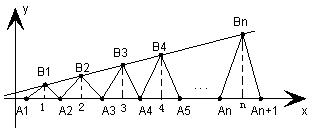
已知点列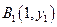
、
、…、
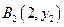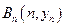（n∈N）顺次为一次函数
图像上的点，点列
、
、…、
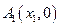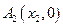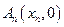（n∈N）顺次为x轴正半轴上的点，其中
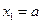（0＜a＜1），对于任意n∈N，点
、
、
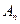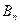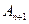构成一个顶角的顶点为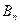的等腰三角形。
（1）数列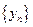
的通项公式，并证明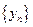是等差数列；
（2）证明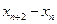
为常数，并求出数列
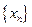的通项公式；
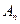
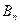
（3）上述等腰三角形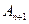中，是否存在直角三角形？若有，求出此时a值；若不存在，请说明理由。
（本小题满分12分） 已知函数
．
（1）当
时，求函数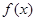
的单调区间和极值；
（2）对任意给定的正实数
，曲线
上是否存在两点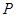
，
，使得△
是以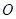
为直角顶点的直角三角形，且此三角形斜边中点在
轴上？
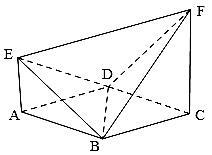
（本小题满分12分）如右图，已知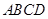
是边长为2的正方形，
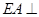平面，
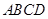，设
，
．
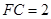（1）证明：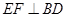
；
（2）求四面体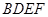
的体积；
（3）求点
到平面
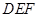的距离．
（本小题满分12分）某同学用“五点法”画函数
（
，
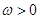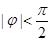）在某一个周期内的图象时，列表并填入了部分数据，如下表：
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
|
 |
 |
|
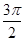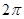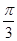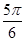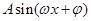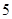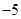（1）请将上表数据补充完整，并求出函数
的解析式；
（2）将
的图象向左平移
个单位，得到函数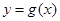
的图象．若关于的方程
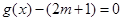在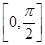
上有两个不同的解，求实数
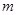的取值范围．
（本小题满分12分） 如图，在△
中，
为
边上一点，
，已知
，
．
（1）若△是锐角三角形，
，求角
的大小；
（2）若△
的面积为
，求边的长．
（本小题满分12分） 已知等差数列
的前
项和
满足
，
．
（1）求的通项公式；
（2）求数列
的前项和．