(本题14分)如图,在三棱锥S ABC中,
ABC中,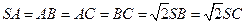 ,O为BC的中点.
,O为BC的中点.
(I)求证: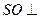 面ABC;
面ABC;
(II)求异面直线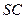 与AB所成角的余弦值;
与AB所成角的余弦值;
(III)在线段AB上是否存在一点E,使二面角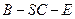 的平面角的余弦值为
的平面角的余弦值为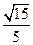 ;若存在,求
;若存在,求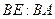 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。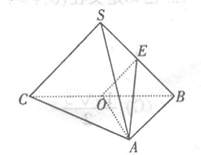
已知数列{ }满足
}满足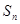 +
+ =2n+1
=2n+1
(1)求出 ,
,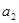 ,
, 的值;
的值;
(2)由(1)猜想出数列{ }的通项公式
}的通项公式 ;
;
(3)用数学归纳法证明(2)的结果.
某公司为了加大产品的宣传力度,准备立一块广告牌,在其背面制作一个形如△ABC的支架,要求∠ACB=60°,BC的长度大于2米,且AC比AB长1米.为节省材料,要求AC的长度越短越好,求AC的最短长度,且当AC最短时,BC的长度为多少米?
如图,直三棱柱 中,
中, 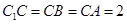 ,
,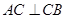 .
. 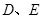 分别为棱
分别为棱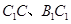 的中点.
的中点.
(1)求二面角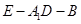 的平面角的余弦值;
的平面角的余弦值;
(2)在线段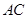 上是否存在一点
上是否存在一点 ,使得
,使得 平
平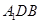 ?
?
若存在,确定其位置;若不存在,说明理由.
设实部为正数的复数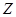 满足
满足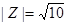 ,且
,且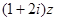 在复平面上对应的点在第一、三象限的角平分线上.
在复平面上对应的点在第一、三象限的角平分线上.
(1)求复数Z;
(2)若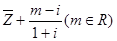 为纯虚数 , 求
为纯虚数 , 求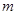 的值.
的值.
已知正项等比数列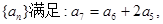 若存在两项
若存在两项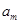 、
、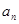 使得
使得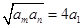 ,且有
,且有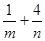 ≥
≥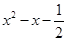 对上述
对上述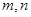 恒成立,求x的取值范围.
恒成立,求x的取值范围.