(本小题满分12分)已知 ,设P:函数
,设P:函数 在R上递增,Q:复数Z=(
在R上递增,Q:复数Z=( -4) +
-4) +  i所对应的点在第二象限。如果P且Q为假,P或Q为真,求
i所对应的点在第二象限。如果P且Q为假,P或Q为真,求 的取值范围。
的取值范围。
(本小题满分14分)
为了进一步实现节能,在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外
墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热
层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)。与隔热层
厚度x(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为8万元;设f(x)为
,若不建隔热层,每年能源消耗费用为8万元;设f(x)为
隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
(本小题满分14分)
如图,在四棱锥P-ABCD中,PD上⊥平面ABCD,AD⊥CD,且BD平分∠ADC,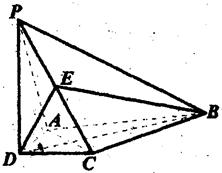 E为PC的中点,AD=CD=l,BC=PC,
E为PC的中点,AD=CD=l,BC=PC,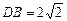
(Ⅰ)证明PA∥平面BDE;
(Ⅱ)证明AC⊥平面PBD:
(Ⅲ)求四棱锥P-ABCD的体积,
(本小题满分12分)
在平面直角坐标系xOy中,点A(-l,-2)、B(2,3)、C(-2,-1)。
(Ⅰ)求以线段AB、AC为邻边的平行四边形两条对角线的长:
(Ⅱ)设实数t满足 ,求t的值。
,求t的值。
(本小题满分12分)
己知函数 ,且f(0)=2,
,且f(0)=2,
(Ⅰ)求f(x)的最大值与最小值;
(Ⅱ)求f(x)的单调增区间.
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为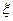 .
.
(Ⅰ)求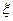 的分布列;
的分布列;
(Ⅱ)求1件产品的平均利润(即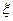 的数学期望);
的数学期望);
(Ⅲ)经技术革新后,仍有四个等级的产品,但次品率降为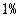 ,一等品率提高为
,一等品率提高为 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?