某同学练习投篮,已知他每次投篮命中率为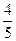 ,
,
(1)求在他第三次投篮后,首次把篮球投入篮框内的概率;
(2)若想使他投入篮球的概率达到0.99,则他至少需投多少次?(lg2=0.3)
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF、△CDE是等边三角形,CD=1,EF=BC=1,EF//BC,M为EF的中点.
(1)证明MO⊥平面ABCD
(2)求二面角E—CD—A的余弦值
(3)求点A到平面CDE的距离
已知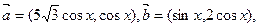 其中
其中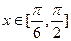 ,
,
设函数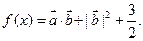
(Ⅰ)求函数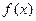 的的值域;
的的值域;
|
(Ⅱ)若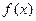 ="8," 求函数
="8," 求函数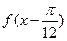 的值.
的值.
已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
(I)求动点D的轨迹E的方程;
(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明.
已知某公司生产品牌服装的年固定成本是10万元,每生产千件,须另投入2.7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为
R(x)万元,且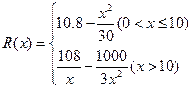
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大?
(注:年利润=年销售收入-年总成本)
设a为实数,函数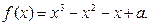
(Ⅰ)求 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线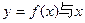 轴仅有一个交点.
轴仅有一个交点.