设函数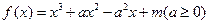 .
.
(1)求函数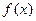 的单调区间;
的单调区间;
(2)若函数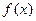 在
在 内没有极值点,求
内没有极值点,求 的取值范围;
的取值范围;
(3)若对任意的 ,不等式
,不等式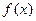 ≤
≤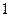 在
在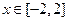 上恒成立,求
上恒成立,求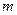 的取值范围.
的取值范围.
已知函数f(x)=ex-e-x(x R)
R)
(1)求证:当x≥0时, ;
;
(2)试讨论函数H(x)=f(x)-ax(x R)的零点个数.
R)的零点个数.
已知直线x+y-1=0经过椭圆C:  的顶点和焦点F.
的顶点和焦点F.
(1)求此椭圆的标准方程;
(2)斜率为k,且过点F的动直线 与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证:直线BD过顶点.
与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证:直线BD过顶点.
某市共有100万居民的月收入是通过“工资薪金所得”得到的,如图是抽样调查后得到的工资薪金所得X的频率分布直方图。工资薪金个人所得税税率表如表所示。表中“全月应纳税所得额”是指“工资薪金所得”减去3500元所超出的部分(3500元为个税起征点,不到3500元不缴税)。
工资个税的计算公式为:“应纳税额”=“全月应纳税所得额”乘以“适用税率”减去“速算扣除数”。
| 全月应纳税所得额 |
适用税率(%) |
速算扣除数 |
| 不超过1500元 |
3 |
0 |
| 超过1500元至4500元 |
10 |
105 |
| 超过4500元至9000元 |
20 |
555 |
| … |
… |
… |
例如:某人某月“工资薪金所得”为5500元,则“全月应纳税所得额”为5500-3500=2000元,应纳税额为2000 10%-105=95(元)
10%-105=95(元)
在直方图的工资薪金所得分组中,以各组的区间中点值代表该组的各个值,工资薪金所得落入该区间的频率作为x取该区间中点值的概率
(1)试估计该市居民每月在工资薪金个人所得税上缴纳的总税款;
(2)设该市居民每月从工资薪金所得交完税后,剩余的为其月可支配额y(元),试求该市居民月可支配额y的数学期望。
如图,正方体ABCD-A1B1C1D1中,E是AB的中点.
(1)在B1C上是否存在点P,使PB∥平面B1ED,若存在,求出点P的位置,若不存在,请说明理由;
(2)求二面角D-B1E-C的平面角的余弦值.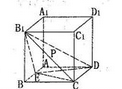
已知△ABC中,a,b,c分别为角A,B,C的对边,a2+b2<c2,且sin(2C-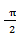 )=
)=
(1)求角C的大小;
(2)求 的取值范围。
的取值范围。