(本小题满分13分)
甲、乙两人各射击一次,击中目标的概率分别是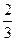 和
和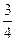 ,假设两个射击是否击中目标,相互之间没有影响;每人各次射击是否中目标相互之间也没有影响。
,假设两个射击是否击中目标,相互之间没有影响;每人各次射击是否中目标相互之间也没有影响。
(1)求甲射击4次,至少有1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则中止其射击。则乙恰好射击5次后被中止射击的概率是多少?
已知函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时,
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
已知集合 ,
,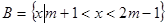
(Ⅰ)若 =5,求
=5,求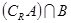 ;
;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
已知平面向量 ,
,
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)若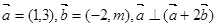 ,求
,求 的值.
的值.
已知半径为 的圆的圆心在
的圆的圆心在 轴上,且与直线
轴上,且与直线 相切.圆心的横坐标是整数。
相切.圆心的横坐标是整数。
(1)求圆的方程;
(2)设直线
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线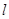 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.