（本小题满分10分）请选做一题，都做时按先做的题判分，都做不加分.
（1）已知向量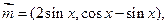
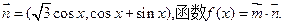
①求函数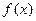
的最小正周期和值域；
②在△ABC中，角A、B、C所对的边分别是a、b、c，若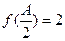
且
，试判断△ABC的形状.
（2）已知锐角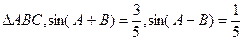
.
①求证：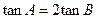
；
②设
，求AB边上的高CD的长.
某英语学习小组共12名同学进行英语听力测试，随机抽取6名同学的测试成绩（单位：分），用茎叶图记录如下，其中茎为十位数，叶为个位数.
（1）根据茎叶图计算样本均值；
（2）成绩高于样本均值的同学为优秀，根据茎叶图估计该小组12名同学中有几名优秀同学；
（3）从该小组12名同学中任取2人，求仅有1人是来自随机抽取6人中优秀同学的概率.
设向量
，
，
，函数
.
（1）求函数
的最小正周期；
（2）在锐角
中，角
、
、
所对的边分别为
、
、
，
，
，
，求的值.
等比数列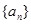
的前
项和
，已知
，
，
，
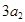成等差数列.
（1）求数列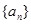的公比
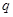和通项
；
（2）若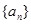是递增数列，令
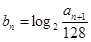，求
.
已知椭圆
的左、右焦点分别为
，且
，长轴的一个端点与短轴两个端点组成等边三角形的三个顶点．
(1)求椭圆方程；
(2)设椭圆与直线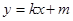
相交于不同的两点M、N，又点
，当
时，求实数m的取值范围，
已知
是二次函数，不等式
的解集是
，且在点
处的切线与直线
平行．
(1)求的解析式；
(2)是否存在t∈N*，使得方程
在区间
内有两个不等的实数根？
若存在，求出t的值；若不存在，说明理由．