:某商店投入38万元经销某种纪念品,经销时间共60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这一产品期间第 天的利润
天的利润 (单位:万元,
(单位:万元,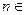
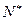 ),记第
),记第 天的利润率
天的利润率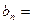
 ,例如
,例如
(1)求 的值;
的值;
(2)求第 天的利润率
天的利润率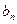 ;
;
(3)该商店在经销此纪念品期间,哪一天的利润率最大?并求该天的利润率.
某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y(万元)随医疗总费用x(万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数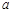 的值.(参考数据:ln2»0.69,ln10»2.3)
的值.(参考数据:ln2»0.69,ln10»2.3)
设 是定义在
是定义在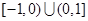 上的函数,当
上的函数,当 ,且
,且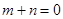 时,有
时,有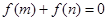 .
.
(1)证明 是奇函数;
是奇函数;
(2)当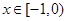 时,
时, (a为实数). 则当
(a为实数). 则当 时,求
时,求 的解析式;
的解析式;
(3)在(2)的条件下,当 时,试判断
时,试判断 在
在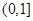 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
设z是虚数,已知ω=z+ 是实数,且-1<ω<2.
是实数,且-1<ω<2.
(1)求|z|的值及z的实部的取值范围;
(2)设u=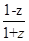 ,求证:u为纯虚数;
,求证:u为纯虚数;
设命题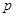 :关于
:关于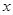 的方程
的方程 无实根;命题
无实根;命题 :函数
:函数 的定义域为
的定义域为 ,若命题"p或q”是真命题,“p且q”是假命题,求实数a的取值范围.
,若命题"p或q”是真命题,“p且q”是假命题,求实数a的取值范围.
已知集合 ,
,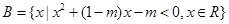 .
.
(1)若 ,求实数
,求实数 的值;
的值;
(2)若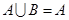 ,求实数
,求实数 的取值范围.
的取值范围.