如图,已知圆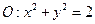 交
交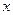 轴于
轴于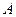 、
、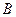 两点,
两点,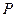 在圆
在圆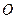 上运动(不与
上运动(不与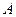 、
、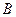 重合),过
重合),过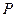 作直线
作直线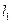 ,
,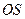 垂直于
垂直于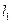 交直线
交直线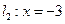 于点
于点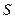 .
.
(1)求证:“如果直线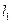 过点
过点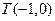 ,那么
,那么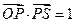 ”为真命题;
”为真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.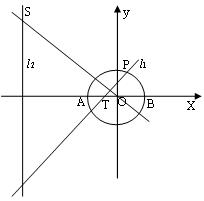
已知椭圆 (a>b>0)的离心率为
(a>b>0)的离心率为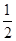 ,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+
,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+ 相切.
相切.
(1)求椭圆的方程;
(2)设直线 与椭圆在
与椭圆在 轴上方的一个交点为
轴上方的一个交点为 ,
, 是椭圆的右焦点,试探究以
是椭圆的右焦点,试探究以 为
为
直径的圆与以椭圆长轴为直径的圆的位置关系.
已知如图:平行四边形ABCD中, ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)若 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.
我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
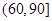 |
 |
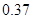 |
 |
 |
 |
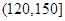 |
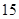 |
 |
| 合计 |
 |
 |
(1)求出表中 、
、 、
、 、
、 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在 分以上的人数;
分以上的人数;
(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
已知函数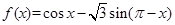 .
.
求函数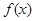 的最小正周期和值域;
的最小正周期和值域;
若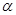 是第二象限角,且
是第二象限角,且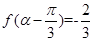 ,试求
,试求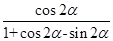 的值.
的值.
设椭圆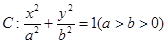 的左、右焦点分别为
的左、右焦点分别为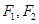 ,
,
上顶点为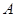 ,在
,在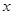 轴负半轴上有一点
轴负半轴上有一点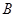 ,满足
,满足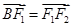 ,且
,且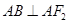 .
.
(Ⅰ)求椭圆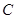 的离心率;
的离心率;
(Ⅱ)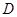 是过
是过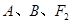 三点的圆上的点,
三点的圆上的点,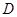 到直线
到直线 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆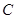 的方程;
的方程;
(Ⅲ)在(Ⅱ)的条件下,过右焦点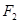 作斜率为
作斜率为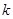 的直线
的直线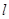 与椭圆
与椭圆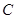 交于
交于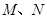 两点,线段
两点,线段 的中垂线与
的中垂线与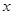 轴相交于点
轴相交于点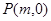 ,求实数
,求实数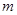 的取值范围.
的取值范围.