某学科的试卷中共有12道单项选择题,(每个选择题有4个选项,其中仅有一个选项是正确的,答对得5分,不答或答错得0分)。某考生每道题都给出了答案,已确定有8道题答案是正确的,而其余的题中,有两道题每题都可判断其两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜。对于这12道选择题,试求:
(1)该考生得分为60分的概率;
(2)该考生所得分数ξ的分布列及数学期望Eξ.
已知椭圆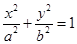 的左焦点
的左焦点 为圆
为圆 的圆心,且椭圆上的点到点
的圆心,且椭圆上的点到点 的距离的最小值为
的距离的最小值为 .
.
(1)求椭圆的方程;
(2)已知经过点 的动直线
的动直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,点
,点 ,求
,求 的值.
的值.
已知圆 过
过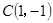 ,
, 两点,且圆心
两点,且圆心 在
在 上.
上.
(1)求圆 的方程;
的方程;
(2)设点 是直线
是直线 上的动点,
上的动点,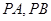 是圆
是圆 的两条切线,
的两条切线, 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值.
某日用品按行业质量标准分成五个等级,等级系数依次为1,2,3,4,5.现从一批日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如表所示:
(1)求 的值;
的值;
(2)从等级为4的2件日用品和等级为5的3件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
已知数列 的前
的前 项和为
项和为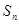 ,且满足
,且满足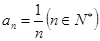 ,若不等
,若不等 对于
对于 恒成立,则自然数
恒成立,则自然数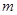 的最大值为
的最大值为
已知 ,且满足
,且满足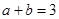 ,则
,则 的最小值为
的最小值为