盒中有5个红球,11个蓝球。红球中有2个玻璃球,3个木质球;蓝球中有4个玻璃球,7个木质球。现从中任取一球,假设每个球摸到的可能性都相同,若已知取到的球是玻璃球,求它是蓝球的概率。
已知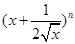 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;
的值;
(2)求展开式中系数最大的项.
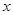 的取值范围为[0,10],给出如图所示程序框图,输入一个数
的取值范围为[0,10],给出如图所示程序框图,输入一个数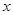 .
.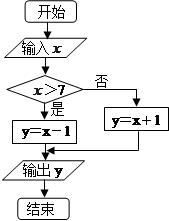
(1)请写出程序框图所表示的函数表达式;
(2)求输出的 (
(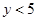 )的概率;(3)求输出的
)的概率;(3)求输出的 的概率.
的概率.
从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下.观察图形,回答下列问题: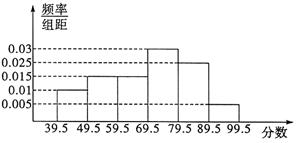
(1)49.5——69.5这一组的频率和频数分别为多少?
(2)估计这次环保知识竞赛成绩的中位数及平均成绩.(精确到小数点后一位)
设函数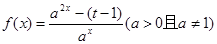 是定义域为
是定义域为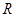 的奇函数.
的奇函数.
(1)求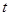 的值;
的值;
(2)若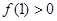 ,求使不等式
,求使不等式 对一切
对一切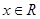 恒成立的实数
恒成立的实数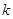 的取值范围;
的取值范围;
(3)若函数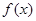 的图象过点
的图象过点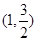 ,是否存在正数
,是否存在正数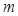 ,且
,且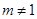 使函数
使函数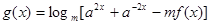 在
在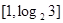 上的最大值为
上的最大值为 ,若存在,求出
,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
设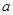 为实数,函数
为实数,函数 ,
,
(1)讨论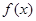 的奇偶性;
的奇偶性;
(2)当 时,求
时,求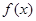 的最大值.
的最大值.