(本小题满分12分)在直角坐标系XOY中,以O为极点,X轴正半轴为极轴建立极坐标系。曲线C的极坐标方程是: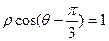 ,M,N分别是曲线C与X、Y轴的交点。
,M,N分别是曲线C与X、Y轴的交点。
(1)写出C的直角坐标系方程。并求M,N的极坐标。
(2)设MN的中点为P,求直线OP的极坐标方程。
(本小题满分14分)
已知圆 的方程为
的方程为 ,定直线
,定直线 的方程为
的方程为 .动圆
.动圆 与圆
与圆 外切,且与直线
外切,且与直线 相切.
相切.
(Ⅰ)求动圆圆心 的轨迹
的轨迹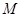 的方程;
的方程;
(II)斜率为 的直线
的直线 与轨迹
与轨迹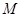 相切于第一象限的点
相切于第一象限的点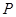 ,过点
,过点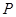 作直线
作直线 的垂线恰好经过点
的垂线恰好经过点 ,并交轨迹
,并交轨迹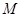 于异于点
于异于点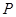 的点
的点 ,记
,记 为
为 (
( 为坐标原点)的面积,求
为坐标原点)的面积,求 的值.
的值.
(本小题满分14分)
设不等式 确定的平面区域为
确定的平面区域为 ,
, 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取3个整点,求这些整点中恰有2个整点在区域
内任取3个整点,求这些整点中恰有2个整点在区域 的概率;
的概率;
(2)在区域 内任取3个点,记这3个点在区域
内任取3个点,记这3个点在区域 的个数为
的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
如图,已知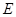 ,
,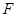 分别是正方形
分别是正方形 边
边 、
、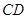 的中点,
的中点,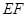 与
与 交于点
交于点 ,
, 、
、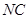 都垂直于平面
都垂直于平面 ,且
,且 ,
,  ,
,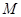 是线段
是线段 上一动点.
上一动点.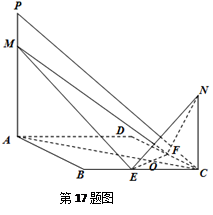
(Ⅰ)求证:平面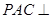 平面
平面 ;
;
(Ⅱ)试确定点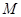 的位置,使得
的位置,使得 平面
平面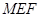 ;
;
(Ⅲ)当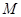 是
是 中点时,求二面角
中点时,求二面角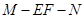 的余弦值.
的余弦值.
(本小题满分12分)
已知函数 (
(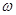 >0,0<
>0,0< )的最小正周期为
)的最小正周期为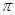 ,且
,且 .
.
(1)求 的值;
的值;
(2)若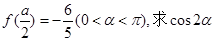
函数

(Ⅰ)当 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(Ⅱ)若 ,若
,若 分别为
分别为 的极大值和极小值,若
的极大值和极小值,若 ,求
,求 取值范围。
取值范围。