过 轴上动点
轴上动点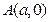 引抛物线
引抛物线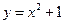 的两条切线
的两条切线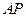 、
、 ,
, 、
、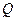 为切点.
为切点.
(Ⅰ)若切线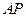 ,
, 的斜率分别为
的斜率分别为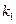 和
和 ,求证:
,求证: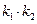 为定值,并求出定值;
为定值,并求出定值; (Ⅱ)求证:直线
(Ⅱ)求证:直线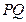 恒过定点,并求出定点坐标;
恒过定点,并求出定点坐标;
(Ⅲ)当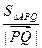 最小时,求
最小时,求 的值.
的值.
(本小题满分14分)设正数数列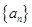 的前n项和为
的前n项和为 ,且满足
,且满足 (
( )
)
(1)求证: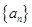 是等差数列;
是等差数列;
(2)设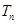 为数列{
为数列{ }的前n项和,求
}的前n项和,求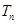 ;
;
(3)设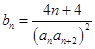 ,证明:
,证明: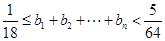 .
.
(本小题满分14分) 如图所示,平面
 平面
平面 ,且四边形
,且四边形 为
为
正方形,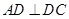 ,
, ∥
∥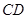 ,
, ,
, 为
为 的中点.
的中点.
(1)求证: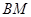 ∥平面
∥平面 ;
;
(2)求证: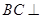 平面
平面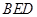 ;
;
(3)求平面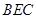 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(本小题满分12分)广东某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取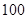 名学生的成绩,按成绩分组:第
名学生的成绩,按成绩分组:第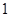 组
组 ,第
,第 组
组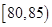 ,第
,第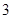 组
组 ,第
,第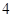 组
组 ,第
,第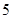 组
组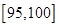 得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第
得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第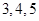 组中用分层抽样抽取
组中用分层抽样抽取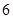 名学生进入第二轮面试.
名学生进入第二轮面试.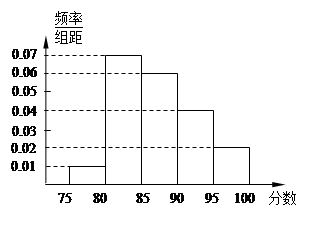
(1)求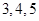 组各应该抽取多少人进入第二轮面试;
组各应该抽取多少人进入第二轮面试;
(2)学校决定在(1)中抽取的这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有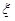 名学生被考官D面试,求
名学生被考官D面试,求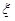 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知函数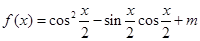 ,当
,当 时,函数
时,函数 的最大值为
的最大值为 .
.
(1)求函数 的值;
的值;
(2)若 ,求
,求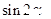 的值.
的值.
(本小题满分14分)已知函数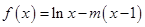 (
(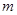 为常数且
为常数且 ).
).
(1)求函数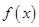 的单调区间.
的单调区间.
(2)若函数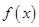 在点
在点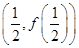 处的切线与直线
处的切线与直线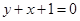 相互垂直.
相互垂直.
①求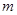 的值;
的值;
②在①的条件下,证明:对于任意的 ,都有
,都有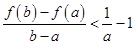 成立.
成立.