已知函数 (其中
(其中 )的图像与x轴的交点中,相邻两个交点之间的距离为
)的图像与x轴的交点中,相邻两个交点之间的距离为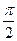 ,且图像上一个最低点为
,且图像上一个最低点为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)当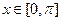 ,求
,求 的单调增区间.
的单调增区间.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.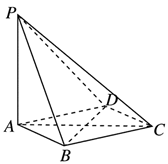
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.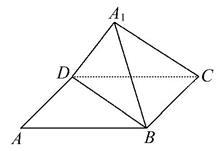
(1)求证:BC⊥A1D.
(2)求证:平面A1BC⊥平面A1BD.
(3)求三棱锥A1-BCD的体积.
已知点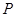 (0,5)及圆
(0,5)及圆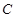 :
: .
.
(1)若直线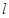 过
过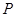 且被圆C截得的线段长为4
且被圆C截得的线段长为4 ,求
,求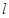 的方程;
的方程;
(2)求过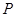 点的圆
点的圆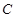 的弦的中点的轨迹方程.
的弦的中点的轨迹方程.
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.
(1)证明:PB∥平面ACM;
(2)证明:AD⊥平面PAC.
(1)求与直线 垂直,且与原点的距离为6的直线方程;
垂直,且与原点的距离为6的直线方程;
(2)求经过直线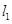 :
: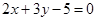 与
与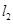 :
: 的交点,且平行于直线
的交点,且平行于直线 的直线方程.
的直线方程.