广东某公司为了应对美国次贷案所造成的全球性金融危机,决定适当进行裁员.已知这家公司现有职工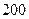 人,每人每年可创利润10万元.根据测算,在经营条件不变的前提下,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利润0.1万元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利润0.12万元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的70%.为保障被裁员工的生活,公司要付给被裁员工每人每年2万元的生活费.设公司裁员人数为
人,每人每年可创利润10万元.根据测算,在经营条件不变的前提下,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利润0.1万元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利润0.12万元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的70%.为保障被裁员工的生活,公司要付给被裁员工每人每年2万元的生活费.设公司裁员人数为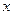 ,公司一年获得的纯收入为
,公司一年获得的纯收入为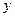 万元.(注:年纯收入
万元.(注:年纯收入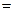 年利润–裁员员工的生活费)
年利润–裁员员工的生活费)
(1)求出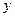 与
与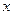 的函数关系式;
的函数关系式;
(2)为了获得最大的经济效益,该公司应裁员多少人?
已知曲线
的参数方程为
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
。
(Ⅰ)把
的参数方程化为极坐标方程;
(Ⅱ)求
与
交点的极坐标
【选修4-1:几何证明选讲】
如图,直线
为圆的切线,切点为
,点
在圆上,
的角平分线BE交圆于点
,
垂直
交圆于
.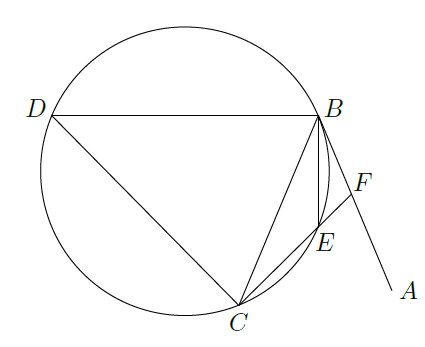
(Ⅰ)证明:
;
(Ⅱ)设圆的半径为1,
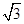 ,延长
交
于点
,求
外接圆的半径.
,延长
交
于点
,求
外接圆的半径.
已知函数 ,若曲线 和曲线 都过点 ,且在点 处有相同的切线 .
(Ⅰ)求
的值
(Ⅱ)若
时,
,求
的取值范围。
已知圆
,圆
,动圆
与圆
外切并与圆
内切,圆心
的轨迹为曲线
.
(Ⅰ)求
的方程;
(Ⅱ)l是与圆
,圆
都相切的一条直线,l与曲线
交于
两点,当圆
的半径最长时,求
.
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为
。如果
=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果
=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为
(单位:元),求
的分布列及数学期望。