一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为
。如果
=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果
=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为
(单位:元),求
的分布列及数学期望。
已知函数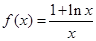 .
.
(1)若函数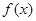 在区间
在区间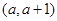 上有极值,求实数
上有极值,求实数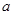 的取值范围;
的取值范围;
(2)若关于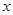 的方程
的方程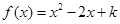 有实数解,求实数
有实数解,求实数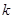 的取值范围;
的取值范围;
(3)当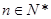 ,
,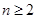 时,求证:
时,求证: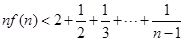 .
.
已知圆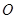 :
: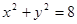 交
交 轴于
轴于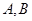 两点,曲线
两点,曲线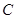 是以
是以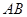 为长轴,直线:
为长轴,直线: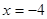 为准线的椭圆.
为准线的椭圆.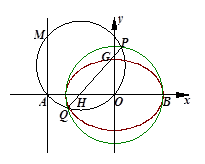
(1)求椭圆的标准方程;
(2)若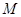 是直线上的任意一点,以
是直线上的任意一点,以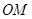 为直径的圆
为直径的圆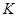 与圆
与圆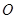 相交于
相交于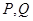 两点,求证:直线
两点,求证:直线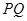 必过定点
必过定点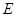 ,并求出点
,并求出点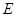 的坐标;
的坐标;
(3)如图所示,若直线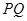 与椭圆
与椭圆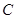 交于
交于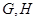 两点,且
两点,且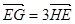 ,试求此时弦
,试求此时弦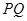 的长.
的长.
设数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,n=1,2,3,…….
,n=1,2,3,…….
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)设 ,求数列
,求数列 的前n项和
的前n项和 .
.
己知某公司生产某品牌服装的年固定成木为10万元,每生产一千件需另投入2.7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每销售一千件的收入为R(x)万元,且
(注:年利润=年销售收入一年总成本)
(1)写出年利润W(万元)关于年产品x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
如图,四边形ABCD是正方形,PB^平面ABCD,MA^平面ABCD,PB=AB=2MA.
求证:(1)平面AMD∥平面BPC;(2)平面PMD^平面PBD.