在一次数学实践活动课上，老师给一个活动小组安排了这样的一个任务：设计一个方案，将一块边长为4米的正方形铁片，通过裁剪、拼接的方式，将它焊接成容积至少有5立方米的长方体无盖容器（只有一个下底面和侧面的长方体）.该活动小组接到任务后，立刻设计了一个方案，如下图所示，按图1在正方形铁片的四角裁去四个相同的小正方形后，将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积，最大容积是多少？是否符合要求？若不符合，请你帮他们再设计一个能符合要求的方案，简单说明操作过程和理由. W ww.k s 5u.c om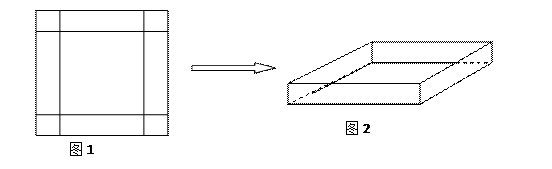
（ 12分 ）已知集合A={x|x2－3x+2=0},B={x|x2－ax+3a－5=0},若A∩B=B，求实数a的值
（ 12分 ）求经过A(-2，-4)且与直线l:x+3y-26=0相切于点B(8，6)的圆的方程.
（ 14分 ）已知圆C：x2+y2-2x+4y-4=0,是否存在斜率为1的直线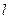
,使以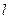被圆C所截得的弦AB为直径的圆经过原点？若存在,写出直线的方程；若不存在,请说明理由.
（ 12分 ）如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.
（ 12分 ）已知汽车从刹车到停车所滑行的距离s(m)与速度v( m/s)的平方及汽车的总重量t(t)的乘积成正比.设某辆卡车不装货物以50 m/s行驶时，从刹车到停车滑行了20 m.如果这辆车装载着与车身相等重量的货物行驶，并与前面的车辆距离为15 m(假设卡车司机从发现前面车辆停车到自己刹车需耽搁1 s)，为了保证前面车辆紧急停车时不与后面车辆撞车，最大限制速度是多少?