已知定义在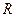 上的函数
上的函数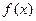 和数列
和数列 满足下列条件:
满足下列条件: ,
,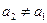 ,当
,当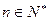 且
且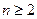 时,
时, 且
且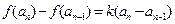 .
.
其中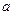 、
、 均为非零常数.
均为非零常数.
(1)若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)令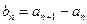
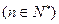 ,若
,若 ,求数列
,求数列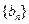 的通项公式;
的通项公式;
(3)试研究数列 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.
已知公差不为零的等差数列 ,等比数列
,等比数列 ,满足
,满足 ,
, ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)若 ,求数列{
,求数列{ }的前n项和.
}的前n项和.
已知函数 ,m∈R,且
,m∈R,且 的解集为
的解集为 .
.
(1)求 的值;
的值;
(2)若 +,且
+,且 ,求
,求 的最小值.
的最小值.
在平面直角坐标系中,已知直线的参数方程是(为参数);以为极点,轴正半轴为极轴的极坐标系中,圆的极坐标方程为.
(1)写出直线的普通方程与圆的直角坐标方程;
(2)由直线上的点向圆引切线,求切线长的最小值.
如图,已知 点在圆
点在圆 直径
直径 的延长线上,
的延长线上, 切圆
切圆 于
于 点,
点, 是
是 的平分线交
的平分线交 于点
于点 ,交
,交 于
于 点.
点.
(1)求 的度数;(2)若
的度数;(2)若 ,求
,求 .
.
已知 .
.
(1)求函数 在
在 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有 成立.
成立.