已知点B(0,1),点C(0,—3),直线PB、PC都是圆 的切线(P点不在y轴上)
的切线(P点不在y轴上)
(I)求过点P且焦点在x轴上抛物线的标准方程;
(II)过点(1,0)作直线 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
(本小题满分12分)已知函数 ,其中A、B、C是
,其中A、B、C是 的三个内角,且满足
的三个内角,且满足 ,
, .
.
(1)求 的值;
的值;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题满分18分)已知数列 ,
, .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)数列 中,是否存在连续的三项,这三项构成等比数列?试说明理由;
中,是否存在连续的三项,这三项构成等比数列?试说明理由;
(3)设 ,其中
,其中 为常数,且
为常数,且 ,
, ,求
,求 .
.
(本小题满分18分)已知函数 ;
;
(1)判断函数奇偶性,并说明理由;
(2)求函数 的反函数
的反函数 ;
;
(3)若函数的定义域为[ ,
, ],值域为
],值域为 ,
, ,并且
,并且 在
在 ,
, 上为减函数.求
上为减函数.求 的取值范围;
的取值范围;
(本小题满分16分)已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ,0).
,0).
(1)求双曲线C的方程;
(2)若直线 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中
(其中 为原点),求
为原点),求 的取值范围。
的取值范围。
(本小题满分14分).已知: (
(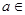
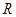 ,
,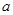 为常数).
为常数).
(1)若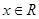 ,求
,求 的最小正周期;
的最小正周期;
(2)若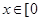 ,
,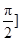 时,
时, 的最大值为4,求
的最大值为4,求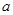 的值.
的值.