(本小题满分12分)如图所示,在长方体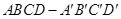 中,
中,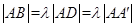 ,(
,(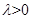 ),
), 、
、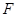 分别是
分别是 和
和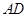 的中点,且
的中点,且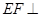 平面
平面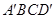 .
.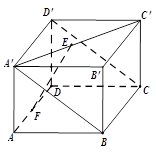
(1)求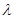 的值;
的值;
(2)求二面角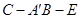 的余弦值.
的余弦值.
如图,已知四棱锥P—ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,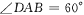 .
.
(I)证明: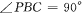 ;
;
(II)若PB = 3,求四棱锥P—ABCD的体积.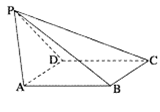
已知函数
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设 的内角
的内角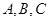 对边分别为
对边分别为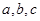 ,且
,且 ,
, ,
,
若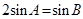 ,求
,求 的值.
的值.
设函数 .
.
(I )求不等式 的解集;
的解集;
(II)若 ,求实数
,求实数 的取值范围.
的取值范围.
已知直线l的参数方程为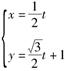 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 为参数).
为参数).
(I )已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II )设点Q是曲线C上的一个动点,求点Q到直线l的距离的最小值与最大值.
如图,四边形ABCD是 的内接四边形,延长BC,AD交于点E,且CE=AB=AC,连接BD,交AC于点F.
的内接四边形,延长BC,AD交于点E,且CE=AB=AC,连接BD,交AC于点F.
(I)证明:BD平分 ;
;
(II)若AD=6,BD=8,求DF的长.